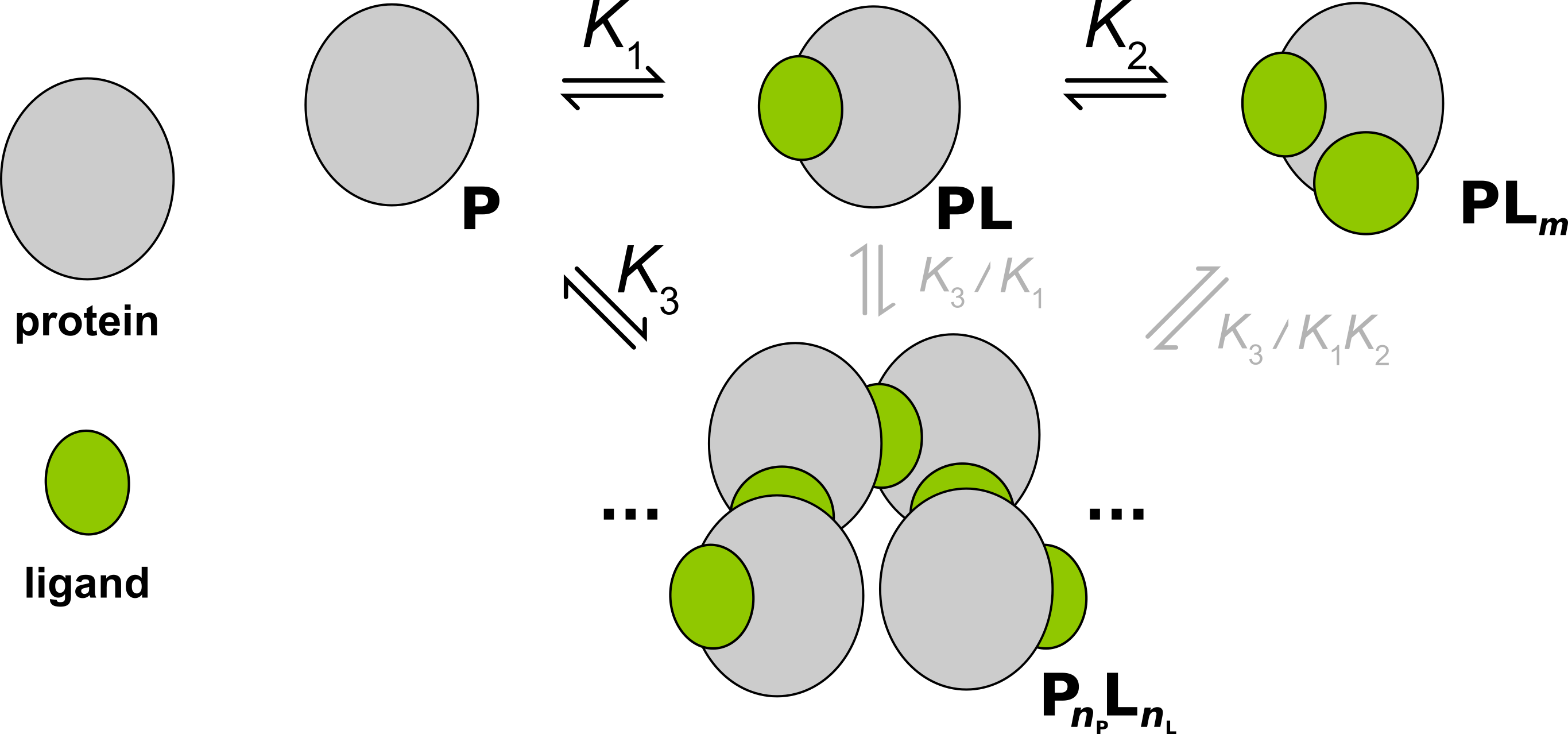
Assembly Auto Inhibition¶
- Ligand binding that promotes protein oligomerization, which is auto-inhibited by saturation of ligand (related to the prozone effect).
- Model contributed by: Martin Rennie, PhD
- Rennie & Crowley (2019). ChemPhysChem (link).
- indiv_models.AssemblyAutoInhibition
Parameters¶
| parameter | variable | parameter name | class |
|---|---|---|---|
| macroscopic association constant for binding of the first ligand to the protein monomer (M-1) | \(K_{1}\) | Klig1 |
thermodynamic |
| average* association constant for binding of the remaining ligands to the protein monomer (M-1) | \(K_{2}\) | Klig2 |
thermodynamic |
| average* association constant for formation of the protein oligomer (M-1) | \(K_{3}\) | Kolig |
thermodynamic |
| enthalpy change for binding of the first ligand to the protein monomer | \(\Delta H_{1}\) | dHlig1 |
thermodynamic |
| enthalpy change for binding of the remaining ligands to the protein monomer | \(\Delta H_{2}\) | dHlig2 |
thermodynamic |
| enthalpy change for formation of the protein oligomer | \(\Delta H_{3}\) | dHolig |
thermodynamic |
| stoichiometry of ligands in the saturated protein monomer, must be ≥2 | \(m\) | m |
thermodynamic |
| stoichiometry of ligands in the protein oligomer | \(n_{L}\) | n_lig |
thermodynamic |
| stoichiometry of proteins in the protein oligomer | \(n_{P}\) | n_prot |
thermodynamic |
| fraction competent protein | — | fx_prot_competent |
nuisance |
| fraction competent ligand | — | fx_lig_competent |
nuisance |
| slope of heat of dilution | — | dilution_heat |
nuisance |
| intercept of heat of dilution | — | dilution_intercept |
nuisance |
*equilibrium constants for the higher order equilibria are “averaged” using \(\sqrt[N]{K}\), where \(N\) is the order of the equilibrium, such that the units are M-1 (see Rennie & Crowley (2019). ChemPhysChem (link))
Species¶
\[[P_{T}]_{i} = [P]_{i} + [PL]_{i} + [PL_{m}]_{i} + n_{P}[P_{olig}]_{i}\]
\[[L_{T}]_{i} = [L]_{i} + [PL]_{i} + m[PL_{m}]_{i} + n_{L}[P_{olig}]_{i}\]
\[[PL]_{i} = K_{1}[P]_{i}[L]_{i}\]
\[[PL_{2}]_{i} = K_{1}K_{2}^{m-1}[P]_{i}[L]_{i}^{m}\]
\[[P_{olig}]_{i} = K_{3}^{n_{L}+n_{P}-1}[P]_{i}^{n_{P}}[L]_{i}^{n_{L}}\]
Heat¶
\[\begin{split}q_{i} = V_{cell}\Big ( \Delta H_{1}^{\circ}([PL]_{i} - [PL]_{i-1}(1-v_{i}/V_{cell})) \\
+ (\Delta H_{1}^{\circ} + \Delta H_{2}^{\circ})([PL_{2}]_{i} - [PL_{2}]_{i-1}(1 - v_{i}/V_{cell})) \\
+ \Delta H_{3}^{\circ}([P_{olig}]_{i} - [P_{olig}]_{i-1}(1 - v_{i}/V_{cell})) \Big ) + q_{dil}\end{split}\]
where: \([P_{T}]_{i}\) is the total cell concentration of protein at the \(i^\text{th}\) injection (independent variable); \([L_{T}]_{i}\) is the total cell concentration of ligand at the \(i^\text{th}\) injection (independent variable); \(V_{cell}\) is the volume of the cell; \(v_{i}\) is the volume of the \(i^\text{th}\) injection; \(q_{i}\) is the heat generated from the \(i^\text{th}\) injection; \(q_{dil}\) is the heat of dilution.