Statistics¶
Warning
pytc will fit all sorts of complicated models to your data. It is up to you to make sure the fit is justified by the data. You should always follow best practices for selecting the your model (choosing the simplest model, inspecting residuals, knowing the assumptions made, etc.)
Fit Results¶
After you have peformed the fit, there are a variety of ways to access and assess your results. These are available for all fit strategies.
Parameter estimates as csv¶
g.fit_as_csv
where g is a GlobalFit
instance. This will print something like:
# Fit successful? True
# 2017-05-13 09:27:25.177062
# Fit type: maximum likelihood
# AIC: -96.23759423779696
# AICc: -93.8028116291013
# BIC: -84.30368995841131
# F: 292708.2585218862
# Rsq: 0.9999672039142115
# Rsq_adjusted: 0.9999637876552752
# ln(L): 54.11879711889848
# num_obs: 54
# num_param: 5
# p: 1.1102230246251565e-16
type,name,exp_file,value,stdev,bot95,top95,fixed,guess,lower_bound,upper_bound
local,dilution_heat,ca-edta/tris-01.DH,1.15715e+03,4.65377e+02,2.21447e+02,2.09285e+03,False,0.00000e+00,-inf,inf
local,K,ca-edta/tris-01.DH,4.05476e+07,4.31258e+05,3.96805e+07,4.14147e+07,False,1.00000e+06,-inf,inf
local,dilution_intercept,ca-edta/tris-01.DH,-6.12671e-01,6.71064e-02,-7.47597e-01,-4.77744e-01,False,0.00000e+00,-inf,inf
local,dH,ca-edta/tris-01.DH,-1.15669e+04,1.00638e+01,-1.15872e+04,-1.15467e+04,False,-4.00000e+03,-inf,inf
local,fx_competent,ca-edta/tris-01.DH,9.73948e-01,8.86443e-05,9.73770e-01,9.74126e-01,False,1.00000e+00,-inf,inf
Lines starting with “#” are statistics and fit meta data. The statistical output is described in the statistics section below. Rendered as a table, the comma- separated output has the following form:
| type | name | exp_file | value | stdev | bot95 | top95 | fixed | guess | lower_bound | upper_bound |
|---|---|---|---|---|---|---|---|---|---|---|
| local | dilution_heat | ca-edta/tris-01.DH | 1.15715e+03 | 4.65377e+02 | 2.21447e+02 | 2.09285e+03 | False | 0.00000e+00 | -inf | inf |
| local | K | ca-edta/tris-01.DH | 4.05476e+07 | 4.31258e+05 | 3.96805e+07 | 4.14147e+07 | False | 1.00000e+06 | -inf | inf |
| local | dilution_intercept | ca-edta/tris-01.DH | -6.12671e-01 | 6.71064e-02 | -7.47597e-01 | -4.77744e-01 | False | 0.00000e+00 | -inf | inf |
| local | dH | ca-edta/tris-01.DH | -1.15669e+04 | 1.00638e+01 | -1.15872e+04 | -1.15467e+04 | False | -4.00000e+03 | -inf | inf |
| local | fx_competent | ca-edta/tris-01.DH | 9.73948e-01 | 8.86443e-05 | 9.73770e-01 | 9.74126e-01 | False | 1.00000e+00 | -inf | inf |
- type: “local” or “global”
- name: parameter name
- exp_file: name of experiment file
- value: estimate of the parameter
- stdev: standard deviation of parameter estimate
- bot95/top95: 95% confidence intervals of parameter estimate
- fixed: “True” or “False” depending on whether parameter was held to fixed value
- guess: parameter guess
- lower_bound/upper_bound: bounds set on the fit parameter during the fit
Fit and residuals plot¶
g.plot()
where g is a GlobalFit
instance. This will create something like:
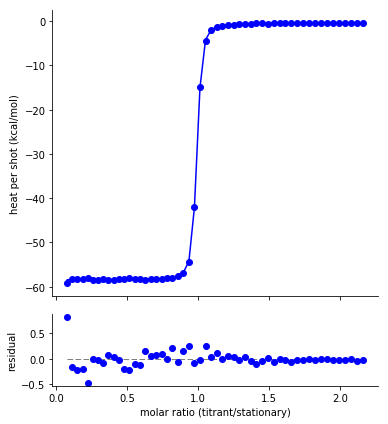
The fit residuals should be randomly distributed around zero, without systematic deviations above or below. Non-random residuals can indicate that the model does not adequately describe the data, despite potentially having a small residual standard error.
Corner plots¶
One powerful way to assess the fit results is through a corner plot, which shows the confidence on each fit parameter, as well as covariation between each parameter. The quality of the histograms is also an indication of whether you have adequate sampling when using the bootstrap or bayesian methods.
g.corner_plot()
where g is a GlobalFit
instance. This will create something like:
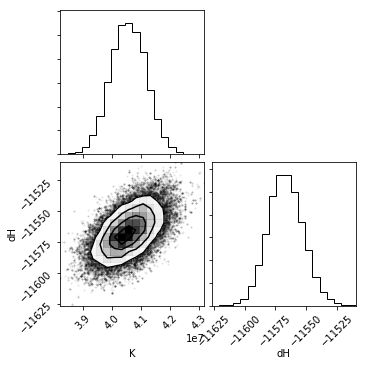
The diagonal shows a histogram for that parameter. The bottom-left cells show a 2D histogram of covariation between those parameters.
g.plot_corner uses keywords to find and filter out nuisance parameters
like fx_competent or dilution_heat. To see these (or modify the
filtering) change the filter_params list passed to the function.
Statistics¶
g.fit_stats
where g is a GlobalFit
instance. This will return a dictionary of fit statistics with the following keys.
- AIC: Akaike Information Criterion
- AICc: Akaike Information Criterion corrected for finite sample size
- BIC: Bayesian Information Criterion
- df: degrees of freedom
- F: The F test statistic
- ln(L): log likelihood of the model
- num_obs: number of data points
- num_param: number of floating parameters fit
- Rsq: \(R^{2}\)
- Rsq_adjusted: \(R^{2}_{adjusted}\)
- Fit type: the type of fit (maxium likelihood, bootstrap, or bayesian)
- Keys like ” bayesian: num_steps” provide information specific to a given fit type.
Model comparison¶
Models with more parameters will generally fit the data better than models with fewer parameters. These extra parameters may or may not be meaningful. (You could, for example, fit \(N\) data points with \(N\) parameters. This would give a perfect fit – and very little insight into the system). A standard approach in model fittng is to choose the simplest model consistent with the data. A variety of statistics can be used to balance fitting the data well against the addition of many parameters. pytc returns four test statistics that penalize models based on the number of free parameters: Akaike Information, corrected Akaike Information, Bayesian Information, and the F-statistic.
The pytc.util.compare_models function will conveniently compare a
collection of models, weighting them by AIC, AICc, and BIC.